
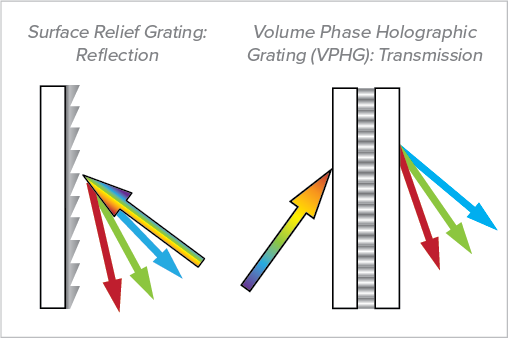
The next point of minimum intensity would be 2λ and so on. If this path difference is λ, a sin θ = λ \sin \theta=\lambda sin θ = λ. The path difference between two maxima s = a sin θ s=a \sin \theta s = a sin θ. To find the other points of maxima and minima, let y be the distance between the brightest maxima and the next one and D be the distance between the screen and aperture. The secondary waves constructively interfere and thus result in maximum intensity. Thus, the path difference between both is zero. The secondary waves from equidistant points form the center of aperture that travels the same distance in reaching the screen’s bright point. The analysis will be restricted to a rectangular grating profile as shown in Fig. Each point on the unblocked portion of a plane wave front sends a secondary wavelet in all directions. r(x) is the complex reflectivity as a function of the coordinate x running perpendicular to the grating bars in the plane of the grating. This is considered to be made up of a set of parallel wavefronts.
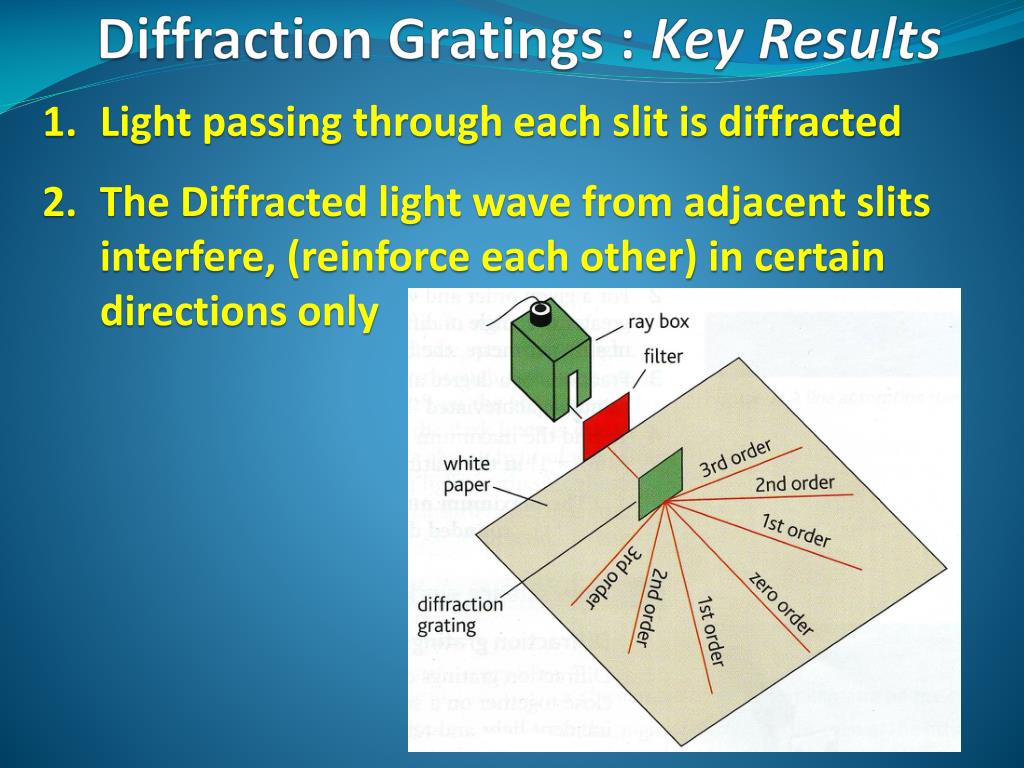
A pattern of light is obtained on the screen, which consists of a central bright band that has alternate dark and weak bands of decreasing intensity on both sides. The experimental set up that is used for diffraction consists of a monochromatic light that is allowed to pass through a single slit and then falls on the screen. This deviation is very important for the comparison of the wavelength of light that is used to the width of the slit or the dimension of aperture. When the wave nature of light is considered, it bends around the corners of the obstacle and thus deviates from its linear path. Light has a dual nature, that is, light can behave as a wave as well as a particle.


 0 kommentar(er)
0 kommentar(er)
